Notions scientifiques
Vues en roller danse.
Calcul mental
Les entrainements et spectacles de roller danse permettent de s’exercer à des opérations simples de calcul mental (+ - x ÷) comme des additions et multiplications (calcul de sommes et de moyennes des notes du jury) ou encore des conversions entre des degrés et des tours: Par exemple, à combien de tours correspondent un 180° ? 360° ? 720° ? 1080° ? À combien de degré correspond un tour et demi?
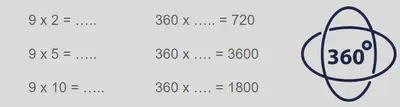
Autre exemple d’exercice: Nous bénéficions de 10% de remise sur les rollers et protections chez Decathlon Pro. Combien coûte un panier de 150€ après réduction? Est-il plus intéréssant de commander chez Hawai Surf le même panier à 120€ (+ frais de port de 10%)?
Géométrie plane et dans l’espace
Apprendre à avancer, reculer ou encore freiner permet d’aborder des notions de géométrie plane et géométrie dans l’espace:
- Les notions de points, de segments, de droites, de courbes et de polygone sont vues dans la construction de parcours.
- Les notions d’angles (aigu, optu, droit), de droites parallèles et perpendiculaires sont incarnées par la position relative et l’orientation des pieds ou des mains.
- La notion de périmètre d’un carré ou d’une roue, en fonction de son rayon, permet de convertir des tours par minutes en km par heure à l’aide de la formule $p=2\pi r$. Les notions de surface, d’aire et de volume sont aussi introduites à l’aide d’objets du quotidien.
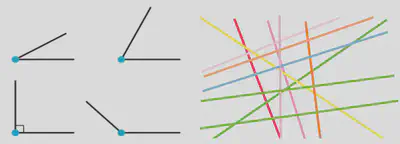
Mathématiques discrètes et suites
Alors que la notion de suite pose des difficultés aux étudiants en lycée, le roller permet de voir, de manière concrète, quelques notions de mathématiques discrètes comme les suites des nombres paires / impaires ou encore d’étudier des distances à parcourir en fonction du nombre de plots.
Exemple d’exercice: Nous espaçons des plots de 50 cm pour apprendre à slalomer. À quelle distance correspondent 7 plots? Combien de plots faut-il pour atteindre 12m? Si Souheila franchit les 10 plots en 30 secondes, quelle est sa vitesse en m/s? Exprimer ce résultat en km/h. Comparer cette vitesse à celle d’une petite brise (voir l’échelle de Beaufort).
Mécanique et cinématique
Le roller met naturellement en jeu des durées, des distances, et donc des vitesses avec la relation $v=\frac{D}{\Delta T}$. Le sport met aussi en avant des forces (gravitation, frottements) et des énergies qui ont de nombreuses applications en mécanique comme le principe d’inertie. Le roller permet aussi d’étudier différentes unités en physique chimie (longueurs, surfaces, volumes, distances, vitesses, accélération, etc.).
Sciences des matériaux
L’entretien des rollers et des roulements permet d’étudier différents matériaux, avec différentes propriétés comme l’acier ou la céramique (densité, masse, résistance au sel, etc.).
Anatomie et sciences du vivant
Les échauffements (et les bobos) permettent de mettre des noms sur des muscles, des os, des ligaments et expliquer leurs liens et l’utilité de chaque protection.
