Introduction à l’analyse (partie I).
Introduction aux suites réelles
Les suites peuvent modéliser des phénomènes discrets, comme l’évolution du stock de livres d’une médiathèque à l’année $n$, $n+1$… (temps discret) ou l’évolution d’une population en écologie (on peut citer les modèles de Malthus et de Verhulst en dynamiques de populations, ou encore les modèles de proie prédateur avec 2-3 suites récurrentes couplées). Ce dernier cas permet d’étudier par exemple l’effet de la réintroduction de loups dans le parc de Yellowstone.
Représentations d’une suite
Formule explicite
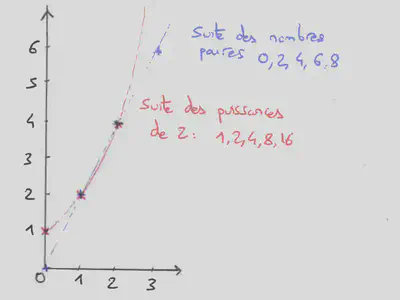
Certaines suites peuvent s’écrire comme des fonctions définies sur l’ensemble des entiers naturels. Pour tout entier naturel $n$, \begin{equation*} u_{n}=f(n) \end{equation*} Par exemple, $u_n=2 \times n$ permet de définir la suite des nombres paires 0, 2, 4… notée $u_0$, $u_1$, $u_2$… La fonction $f$ dépend du problème étudié. Lorsqu’elle est explicite, on peut calculer les termes d’une suite en remplacant $n$ dans l’expression $u_n = f(n)$. Par exemple, pour calculer $u_3$ il suffit de calculer $u_3=2 \times 3 = 6$. On peut aussi lire $u_3$ graphiquement à partir de la courbe représentative de $f$.
Relation de récurrence
Certaines suites s’écrivent à l’aide d’une condition initiale (premier terme donné $u_0 = a$) et d’une relation de récurrence qui traduit une évolution: Pour tout entier naturel $n$, \begin{equation*} \begin{array}{l} u_{n+1} = u_n + gains - pertes \end{array} \end{equation*} Par exemple, $u_{0}=0$ et $u_{n+1} = u_n +2$ permet de définir la suite des nombres paires 0, 2, 4… Autre exemple, la suite de Fibonacci, définie par $u_0=0$, $u_1=1$ et $u_{n+1}=u_{n}+u_{n-1}$, est reliée au nombre d’or qui a de nombreuses application artistiques, notamment en photographie. On peut aussi modéliser l’évolution d’une population à l’aide de la suite $u_{n+1} = u_n + \tau \times u_n = (1 + \tau) \times u_n $, $\tau$ s’interprête comme le taux d’accroissement.
Pour calculer les termes successifs d’une suite récurrente, il suffit de remplacer $n$ dans l’expression précédente. En prenant $n=0$, on calcule $u_{1}$ à partir du premier terme $u_0$, puis avec $n=1$, on calcule $u_{2}$ à partir de $u_1$, etc. On peut aussi construire successivement $u_1$, $u_2$, $u_3$… graphiquement, en utilisant la droite d’équation $y=x$.
Sens de variation et limite
La suite $(u_n)$ tend vers $+ \infty$, notée $\lim\limits_{\substack{n \to +\infty}} u_n = +\infty$, si tout intervalle de la forme [A;$+\infty$[ contient toutes les valeurs $u_n$ à partir d’un certain entier $n_0$. De manière analogue, on définit une suite qui tend vers $-\infty$.
La suite $(u_n)$ converge vers le réel $l$, notée $\lim\limits_{\substack{n \to +\infty}} u_n = l$, si tout intervalle ouvert contenant $l$ contient toutes les valeurs $u_n$ à partir d’un certain entier $n_0$.
Théorème: Toute suite croissante majorée (ou décroissante minorée) converge.
Corollaire: Toute suite croissante non majorée (ou décroissante non minorée) diverge vers $\pm \infty$.
Suites arithmétiques et géométriques
Une suite arithmétique est une suite dans laquelle chaque terme s’obtient à partir du précédent, en lui ajoutant une constante $\textbf{r}$ appelée raison (ou gain). Une suite géométrique est une suite dans laquelle chaque terme s’obtient à partir du précédent, en le multipliant par un facteur constant $\textbf{q}$ appelé raison (ou gain).
| Suite arithmétique (+) | Suite géométrique (x) | |
|---|---|---|
| Exemple | Les nombres paires $(2n)_{n\in\mathbb{N}}$ | Les puissances $(2^n)_{n\in\mathbb{N}}$ |
| 1er termes | 2,4,6,8… | 2,4,8,16… |
| Formule explicite | $u_{n}=u_{0}+n \times r$ | $u_{n}=u_{0}\times q^{n}$ |
| Récurrence | $u_{n+1}=u_{n}+r$ | $u_{n+1}=q\times u_{n}$ |
| Caractérisation | $u_{n+1}-u_n=r$ (constant) | $\frac{u_{n+1}}{u_n}=q$ (constant) |
| Variations | Constantes | Proportionnelles à $u_n$ |
| Évolution | Linéaire / Affine | Exponentielle |
| Cas particulier | $r=0$ | $q=1$ ou $u_0= 0$ |
| Sens de variation | Dépend de $r$ | Dépend de $u_0$ et $q$ |
| Limite | $\lim\limits_{\substack{n \to +\infty}} u_n = +\infty$ si $r > 0$ | $\lim\limits_{\substack{n \to +\infty}} u_n = 0$ si $\left\lvert q \right\rvert <1$ |
| $\lim\limits_{\substack{n \to +\infty}} u_n = -\infty$ si $r < 0$ | $\lim\limits_{\substack{n \to +\infty}} \left\lvert u_n \right\rvert = +\infty$ si $\left\lvert q \right\rvert >1$ | |
| $u_0 + u_1 + … + u_n = $ | $(n+1)u_0 + \frac{n(n+1)r}{2}$ | $u_{0}{\frac {1-q^{n+1}}{1-q}}$ |
| Cas particulier | $1+2+…+n= \frac{n(n+1)}{2}$ | $1 + q + … + q^n = {\frac {1-q^{n+1}}{1-q}}$ |
Exercices résolus
- Livret de la 1ère à la terminale: Exercices 18 à 28.
- Livret de la terminale au supérieur: Exercices 6.