Introduction à l’analyse (partie II).
Introduction aux fonctions d’une variable réelle
Les fonctions permettent de modéliser et étudier divers phénomènes, issus de la biologie, de la physique, des sciences économiques et sociales… Elle peuvent par exemple modéliser l’évolution du stock de livre d’une médiathèque chaque mois (le temps est discret) ou modéliser des températures et des marées (le temps est continu).
On appelle courbe représentative de la fonction $f$, l’ensemble des points M du plan de coordonnées $(x,y)$ qui vérifient l’équation $y = f(x)$. On dit dans ce cas que le point M appartient à la courbe représentative de f.
On appelle image d’un nombre $x$ par la fonction f, la valeur $f(x)$. Par exemple l’image de 2 par la fonction f est $f(2)$. On peut calculer des images à l’aide de l’expression de $f$ ou à l’aide d’une représentation graphique de $f$.
On appelle antécédent(s) d’un nombre $k$ par la fonction f, les nombres $x$ qui vérifient $f(x)=k$. En particulier, on appelle racine(s) d’une fonction (ou d’une équation, d’un polynome) les antécédents de 0 par la fonction f, c’est à dire les solutions de l’équations $f(x)=0$. On peut calculer des antécédents à l’aide de l’expression de $f$ ou à l’aide d’une représentation graphique de $f$: on cherche les points d’intersection de la courbe représentative de $f$ avec la droite d’équation $y=k$. Un programme ou un tableau de valeur peut aussi être utilisé pour déterminer le nombre de solutions d’une équation du type $f(x) = k$ et déterminer un encadrement ou des valeurs approchées. De même, on peut résoudre algébriquement ou graphiquement une inéquation du type $f(x) \leq k$.
Fonctions usuelles et représentations graphiques
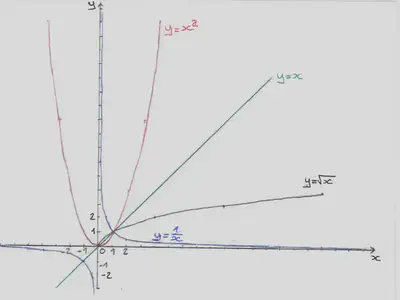
Une fonction affine est une fonction représentée par une droite et qui peut s’écrire sous la forme $f(x)=a \times x + b$ où $a$ et $b$ sont des constantes appelées pente et ordonnée à l’origine. En effet, on a $f(0)=b$. Dans le cas où $b=0$, on l’appelle fonction linéaire, représentée par une droite passant par l’origine O. Dans ce cas la pente $a$ est aussi appelée coefficient de proportionnalité.
On appelle fonction carré la fonction qui à $x$ associe $f(x)=x\times x$ noté $x^2$, représentée par la parabole d’équation $y=x^2$. De même on définit la fonction cube comme la fonction qui à $x$ associe $f(x)=x\times x \times x$ noté $x^3$. Enfin, pour un entier naturel $n$, on appelle fonction puissance n, la fonction qui à $x$ associe $f(x)=x\times … \times x= x^n$ (n fois). On peut généraliser cette définition en notant que $x^{-1}=\frac{1}{x}$ et $x^\frac{1}{2}=\sqrt{x}$. Pour rappel, pour trois nombres entiers $a$, $b$ et $n$, on a les règles suivantes de calcul sur les puissances:
\begin{equation*} 2^a \times 2^b = 2^{a+b} \end{equation*}
\begin{equation*} \frac{2^a}{2^b} = 2^{a-b} \end{equation*}
\begin{equation*} 2^a \times 10^a = (2 \times 10)^a \end{equation*}
\begin{equation*} (2^a)^n = 2^{a \times n} \end{equation*}
On appelle fonction racine carré, notée $f(x)=\sqrt{x}$ ou encore $x^{\frac{1}{2}}$ la fonction réciproque de la fonction carrée, définie pour tout réel $x$ positif. Autrement dit, pour tout nombre $x \geq 0$, $\sqrt{x^2}=x$ et $(\sqrt{x})^2=x$.
On appelle valeur absolue, la fonction qui à $x$ associe $x$ si $x$ est positif et $-x$ sinon, notée $f(x)=|x|$. Elle permet de mesurer la distance entre deux nombres réels. Par exemple, la distance entre 6 et 4 est $|4-6|=|-2|=2$.
On appelle fonction inverse, représentée par une hyperbole, la fonction qui à tout réels $x$ non nul associe $f(x)=\frac{1}{x}$ aussi noté $x^{-1}$.
On appelle fonctions trigonométriques les fonctions cosinus, sinus et tangente.
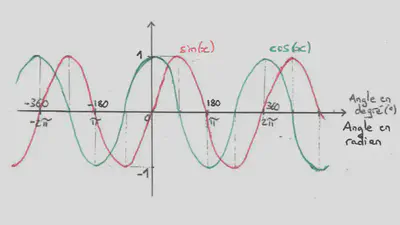
Continuité et limites
On dit qu’une fonction $f$ admet une limite finie $l$ en un point, notée $\lim\limits_{x \to a}f(x)=l$ si tout intervalle ouvert contenant $l$ contient toutes les valeurs $f(x)$ au voisinage de $a$ ou à partir d’un certain rang lorsque $a=\pm \infty$. On dit qu’une fonction $f$ admet une limite infinie en un point si $l=\pm \infty$.
A titre d’exemple, les fonctions carré, cube et racine carrée, tendent vers $+ \infty$ quand x tend vers $+\infty$, et on a les propriétés suivantes sur les limites: Si f et g tendent vers $+\infty$ quand x tend vers $a$, alors $f+g$ et $f\times g$ tendent vers $+\infty$ quand x tend vers $a$. En revanche, on ne peut rien dire de $f-g$ et de $\frac{f}{g}$ (forme indéterminée), cela dépend de la vitesse à laquelle chacun tend vers $+\infty$. De même, si f tend vers $+\infty$ quand x tend vers $a$ et g tend vers $0$, on ne peut rien dire de la limite de $f \times g$ en $a$. Des méthodes existent pour déterminer la limite de formes indéterminées, par exemple en factorisant par le terme prépondérant dans une somme.
On dit que la courbe d’une fonction $f$ admet une asymptote horizontale d’équation $y=l$ si $\lim\limits_{x \to \pm \infty}f(x)=l$. On dit que la courbe d’une fonction $f$ admet une asymptote verticale d’équation $x=a$ si $\lim\limits_{x \to a}f(x)=\pm \infty$. On dit que $f$ admet la droite d’équation $y=a\times x + b$ comme asymptote oblique si la courbe représentative de $f$ tend à se confondre avec la droite quand $x$ tend vers $\pm \infty$.
Notions de continuité
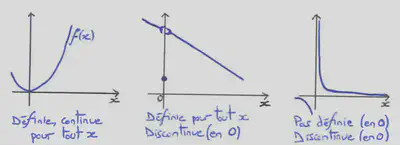
On dit qu’une fonction $f$ est continue en un point $a$ si $\lim\limits_{x \to a}f(x)=f(a)$. On dit que $f$ est continue sur un intervalle si elle est continue en chaque point. Graphiquement, une fonction continue se trace sans lever la main.
Théorème des valeurs intermédiaires: Si $f$ est continue sur $[a,b]$ et $k$ est compris entre $f(a)$ et $f(b)$, alors l’équation $f(x) = k$ admet des solutions (démonstration par dichotomie). Lorsque $f$ est strictement monotone, la solution est unique.
Variations, dérivabilité et extremum
Nombre dérivé (local)
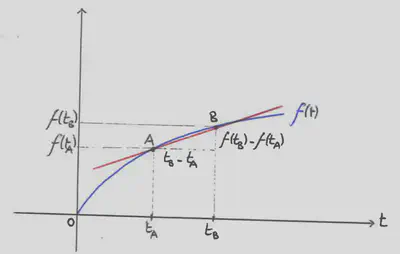
On appelle taux de variation d’une fonction en deux points $A$ et $B$, la pente (ou coefficient directeur) de la droite passant par $A$ et $B$.
Calcul du taux de variation $\tau_{A,B}$ entre A et B:
\begin{equation*} \tau_{A,B} = \frac{f(x_b) - f(x_a)}{x_b-x_a} \end{equation*}
En prenant $x_b=x_a+h$, on obtient
\begin{equation*} \tau_{A,h} = \frac{f(x_a + h) - f(x_a)}{h} \end{equation*}
On appelle nombre dérivé d’une fonction en un point $a$, noté $f’(a)$, la limite du taux de variation à la courbe représentative d’une fonction en un point donné.
\begin{equation*} f’(a) = \lim\limits_{h \to 0} \tau_{A,h} \end{equation*}
Pour les fonctions carré, inverse, racine carrée et fonctions du second degré, on peut faire apparaître une approximation linéaire pour h petit qui permet de calculer le nombre dérivé en un point.
On appelle tangente à la courbe représentative de $f$ au point d’abscisse a, la droite d’équation $y = f(a) + f’(a)(x - a)$ dont la pente $f’(a)$ correspond au nombre dérivé de $f$ en $a$. La tangente est la limite de la droite donné pour un taux d’accroissement. Elle permet d’approximer au mieux la courbe $f$ au voisinage de $a$.
Remarque: Pour une fonction affine, le coefficient directeur correspond au nombre dérivé (constant). S’il est positif, la fonction croit. Sinon, la fonction décroit.
On appelle extremum de la courbe un minimum ou maximum de cette courbe. Il peut être local ou global.
Propriété: Si $f$ est dérivable en $a$ et $a$ est un extremum de la courbe de $f$, alors $f’(a)=0$. Dans ce cas, la tangente à la courbe représentative est horizontale.
Fonction dérivée (globale)}
On dit qu’une fonction $f$ est dérivable sur un intervalle $I$ si elle admet un nombre dérivée en chaque point. Dans ce cas on appelle fonction dérivée la fonction $f’(x)$. Elle est utile pour étudier le sens de variation et les extremums d’une fonction. En effet, si $f’$ est positif, la fonction $f$ croit et si $f’$ est négatif, la fonction $f$ décroit. Ceci permet de dresser un tableau de variations de la fonction $f$ et chercher d’éventuels extremum (problème d’optimisation) en cherchant les antécédants de $0$ par $f’$.
Propriété: Une fonction dérivable sur un intervalle est continue. La réciproque est fausse (exemple de la fonction fonction racine carrée et valeur absolue en 0).
Propriété: Le tableau suivant donne les fonctions dérivées des fonctions usuelles,
| Fonction | Domaine $D_f$ | Dérivée | Domaine $D_{f’}$ |
|---|---|---|---|
| $f(x) = x$ | $\mathbb{R}$ | $f’(x) = 1$ | $\mathbb{R}$ |
| $f(x) = x^2$ | $\mathbb{R}$ | $f’(x) = 2\times x$ | $\mathbb{R}$ |
| $f(x) = x^3$ | $\mathbb{R}$ | $f’(x) = 3\times x^2$ | $\mathbb{R}$ |
| $f(x) = x^n$ | Dépend de n | $f’(x) = n\times x^{n-1}$ | Dépend de n |
On a aussi les propriétés suivantes pour des fonctions dérivables:
\begin{equation*} (f+g)’=f’+g' \end{equation*}
\begin{equation*} (f\times g)’=f’\times g+ f \times g' \end{equation*}
\begin{equation*} (\frac{f}{g})’= \frac{f’\times g - f \times g’}{g^2} \end{equation*}
\begin{equation*} (f(g))’= g’ \times f’(g) \end{equation*}
La dernère égalité, donnée pour calculer la dérivée d’une fonction composée, aussi noté $f o g$, permet de calculer les fonctions dérivées suivantes
| Fonction composée | Dérivée |
|---|---|
| $x \rightarrow f(a\times x + b)$ | $x \rightarrow a\times f’(a\times x + b)$ |
| $x \rightarrow u(x)^2$ | $x \rightarrow 2 \times u(x) \times u’(x)$ |
| $x \rightarrow e^{u(x)}$ | $x \rightarrow u’(x) \times e^{u(x)}$ |
| $x \rightarrow ln(u(x))$ | $x \rightarrow \frac{u’(x)}{u(x)}$ |
Fonctions convexes
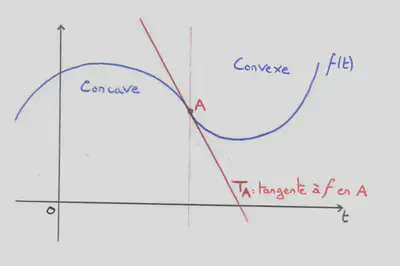
On dit qu’une fonction $f$ est convexe (respectivement concave) sur un intervalle $I$ si la courbe représentative de $f$ est au dessus (respectivement en dessous) de ses sécantes. Lorsque $f$ est dérivable, cela se traduit par la courbe représentative de $f$ est au dessus (respectivement en dessous) de ses tangentes. Cette caractérisation se traduit par la croissance (respectivement la décroissance) de $f’$.
Propriété: Si $f$ est deux fois dérivables sur un intervalle et si $f’’$ est positive, alors la fonction $f$ est convexe et réciproquement. Si $f’’$ est négative, alors la fonction $f$ est concave et réciproquement.
Fonction exponentielle
On appelle fonction exponentielle, notée $f(x)=exp(x)=e^x$, l’unique fonction dérivable sur $\mathbb{R}$ vérifiant $f’ = f$ et $f(0) = 1$. Elle est strictement positive et croissante. Sa limite en $-\infty$ est $0$ et sa limite en $+\infty$ est $+\infty$.
Propriété: Pour tous réels x et y, on a \begin{equation*} e^{x + y} = e^x \times e^y \end{equation*} \begin{equation*} e^{-x} = \frac{1}{e^x} \end{equation*}
On appelle fonction logarithme népérien, notée $f(x)=ln(x)$ la fonction réciproque de la fonction exponentielle, définie pour tout réel $x > 0$. Autrement dit, pour tout nombre $x > 0$, $e^{ln(x)}=x$ et $ln(e^x)=x$. Sa limite en $0$ est $-\infty$ et sa limite en $+\infty$ est $+\infty$.
Propriété: Pour tout entier n, et pour tout réels x et y strictement positifs, on a
\begin{equation*} ln(x \times y) = ln(x) + ln(y) \end{equation*}
\begin{equation*} ln(x^n) = n \times ln(x) \end{equation*}
\begin{equation*} ln(\frac{1}{x})=-ln(x) \end{equation*}
Propriété: Pour tout entier naturel $n>0$,
\begin{equation*} \lim\limits_{x \to 0} x \times ln(x) = 0 \end{equation*}
\begin{equation*} \lim\limits_{x \to +\infty} \frac{ln(x)}{x} = 0 \end{equation*}
\begin{equation*} \lim\limits_{x \to +\infty} \frac{e^x}{x^n} = 0 \end{equation*}
Exercices résolus
- Livret de la 3ème à la 2nde: Exercices 8 à 13 et 61 à 67.
- Livret de la 2nde à la 1ère: Exerices 59 à 73.
- Livret de la 1ère à la terminale: Exerices 33 à 49.
- Livret de la terminale au supérieur: Exerices 4 et 5.